¿Cómo decidir qué método aplicar?

Hay dos cuestiones importantes que deben tenerse en cuenta al evaluar un algoritmo:

• El esfuerzo computacional requerido para ejecutarlo.

• La precisión que este esfuerzo produce.

Para los algoritmos vistos, el mayor esfuerzo se presenta en la evaluación de f. El algoritmo de Euler hace una evaluación de f por paso y el de RK4 hace cuatro, mientras que los de Taylor, tienen la complicación de evaluar las derivadas de f en cada paso. Por esta razón, y dado que un método de Runge-Kutta de orden m tiene la misma precisión que el método de Taylor de igual orden, es que los métodos de Taylor no se utilizan con fines prácticos.

Por lo dicho anteriormente, el método RK4 requiere cuatro veces más esfuerzo por paso. Este hecho puede resultar engañoso ya que suele obtenerse con pocos pasos de RK4 la misma precisión que con cientos del método de Euler. Por ejemplo, analicemos los resultados obtenidos al aplicar ambos procedimientos en el siguiente PVI:
 

La solución exacta de este problema está dada por y = 2 + 2 t + e^t. El valor aproximado de y(1) obtenido con los métodos de Euler y Runge Kutta y con distintos pasos para cada uno de ellos, arrojó los resultados tabulados en la tabla siguiente:

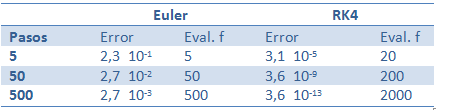
Se observa en esta tabla que al reducir el tamaño del paso en un factor 10, se reduce el error un factor 10 para el método de Euler, y un factor 10000 para el método de Runge-Kutta de orden 4. Esto es consecuencia del error global de cada método. 

 

Consistencia, estabilidad y convergencia

 

Hay algunas propiedades importantes de las ecuaciones en diferencias para problemas de valor inicial de EDOs de primer orden que deben considerarse antes de que se pongan en práctica los métodos numéricos. Ellas son consistencia, estabilidad y convergencia.

 

Se dice que una ecuación en diferencias es consistente con una EDO si la diferencia entre ambas (el error de truncamiento) se acerca a cero a medida que el paso h tiende a cero. En símbolos, si llamamos t_i(h) al error local de truncamiento, podemos decir:

 

Con este concepto se analiza la relación entre la ecuación diferencial y su formulación discreta. Cuando se conoce el error de truncamiento, es fácil probar la consistencia. Cuando no se conoce, debe analizarse la ecuación en diferencias completa para probar la consistencia, utilizando el desarrollo de Taylor.

 

Un método es estable si produce soluciones acotadas cuando la solución exacta es acotada y es inestable cuando produce una solución no acotada cuando la solución exacta es acotada.

 

Hay varias definiciones de estabilidad. Informalmente, se dice que un método es inestable si los errores en las aproximaciones crecen en forma exponencial a medida que el cálculo avanza.

 

Por último, se dice que un método de la ecuación en diferencias de un paso es convergente respecto a la ecuación diferencial que aproxima, si

 

 

Con la convergencia se analiza la relación entre la solución numérica y la solución exacta de la ecuación diferencial. Si se cumplen las condiciones de estabilidad y consistencia en un problema bien planteado, entonces podremos asegurar la convergencia.

 

El método de Runge–Kutta de orden 4 no presenta inestabilidad numérica para valores de h suficientemente pequeños. Pero para el método de Euler estudiado no se puede decir lo mismo.

Por ejemplo, utilicemos este método para resolver el problema:

La solución exacta de esta ecuación está dada por y(t) = e^-t, siendo una función acotada.

 

La ecuación del método de Euler resulta

 

 y_n+1 = y_n + h (- y_n) = (1 – h) y_n = G y_n

 

Aplicando reiteradamente esta fórmula podemos expresar entonces la solución aproximada en función de y₀:

 y_n+1 = (1 – h)ⁿ⁺¹ y₀ , n = 1, …, N.

Se ve en esta ecuación que la solución discreta va a ser acotada siempre que la constante 1-h sea menor a uno en valor absoluto. Esto implica que h debe ser menor a 2, aunque el comportamiento óptimo se da para valores de h entre 0 y 1. Por lo tanto, la solución obtenida con el método de Euler será estable siempre que h sea menor que 2. El hecho de que la estabilidad del método dependa del valor de h, hace que el método sea condicionalmente estable.

Este análisis de estabilidad puede hacerse sólo para ecuaciones diferenciales lineales. En el caso de ecuaciones diferenciales no lineales, deben primero linealizarse localmente, y realizar un análisis de estabilidad en la ecuación de diferencias que aproxima a la ecuación diferencial linealizada.