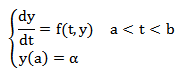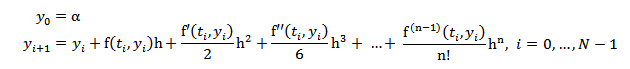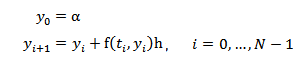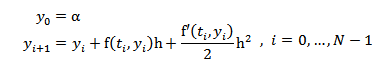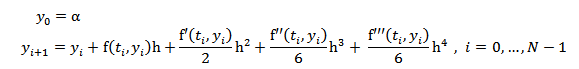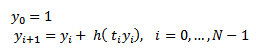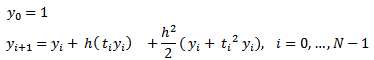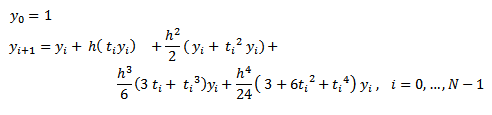Métodos de Taylor
Se presenta de nuevo el problema de valor inicial cuya solución se
intenta aproximar:
|
|
(1) |
Como en el método de Euler, se determina primero la malla {t0, t1, ... , tN} de paso h, donde t0 = a y tN = b. En estos puntos es donde se va a obtener la aproximación de la solución.
El método de Euler se obtuvo aplicando el desarrollo de una función en polinomios de Taylor con n = 1, para aproximar la solución de la ecuación diferencial del problema (1). El error local de este método, dado por el error de la fórmula de Taylor, resultó O(h2), llevando a un error global de O(h). Con el objeto de encontrar un método que mejore las propiedades de convergencia, se pueden utilizar, de la misma manera, polinomios de Taylor de mayor grado.
Se supone que la solución y(t) del problema de valor inicial (1) tiene
(n+1) derivadas continuas. Si se hace un desarrollo de Taylor de la
función y(t) alrededor del punto ti se tiene:
|
|
(2) |
para algún número ξi entre ti y t. Si se evalúa la
expresión (2) en t = ti+1, para cualquier i, y como ti+1 - ti
= h, se tiene, para ξi entre ti y ti+1
|
|
(3) |
Como y satisface la ecuación diferencial, en particular es y'(ti
) = f(ti,yi), y derivando sucesivamente
(teniendo en cuenta que y es función de t, por lo que se deberá aplicar
la regla de la cadena), se
tiene:
-
y''(ti ) = f'(ti, yi) = (ft 1 + fy y')i = (ft + fy f)i
-
y'''(ti ) = f''(ti, yi) = [ftt 1 + fty y' + fyt 1 + fy' f + fy f ']i = [ftt + fty f + (fyt 1 + fyy y')f + fy (ft + fy f)]i
= [ftt + 2fty f + fyy f 2 + fy ft + fy2 f)]i
y en general, y(n)(ti ) = f(n-1)(ti,yi) (utilizando la expresión corta)
Al sustituir estos resultados en la ecuación (3), se obtiene:
|
|
(4) |
La ecuación dada por (4) se llama ecuación de diferencias, y define el método de Taylor de orden n, que se obtiene suprimiendo el término de error que contiene el valor desconocido ξi.
Por lo tanto, la fórmula del método de Taylor de orden n resulta:
|
|
(5) |
Método de Taylor de orden 1
Dado el PVI descripto por la expresión (1) tenemos que el método de
Taylor de orden 1, tomando n = 1 en la fórmula (5), resulta:
|
|
(6) |
Vemos que el método de Taylor de orden 1 resulta ser el método de Euler.
El error local de este método, que obviamente no se conoce, es 1/2 f''(xi) h2, por lo tanto, es O(h2), mientras que el error global resulta ser O(h)
Método de Taylor de orden 2
Según la expresión (5) para n = 2, el método de Taylor de orden 2 es:
|
|
(7) |
Esta fórmula tiene un error local de O(h3), y un error global de O(h2). Es más precisa que la fórmula de Euler, pero requiere el cálculo de la derivada de la función f(t, y).
Método de Taylor de orden 4
Según la expresión (5) para n = 4, el método de Taylor de orden 4 es:
|
|
(8) |
Esta fórmula tiene un error local de O(h5), y un error global de O(h4). Su precisión es mayor que las fórmulas (6) y (7), pero tiene el inconveniente del cálculo de hasta la tercer derivada de f(t, y).
Ejemplo
Sea el problema de valor inicial
![]()
A continuación, se aplican las fórmulas de los métodos de Euler, Taylor de orden 2 y 4 al problema de valor inicial, y se comparan los errores, teniendo en cuenta la solución exacta, que en este caso se puede calcular.
Para obtener las fórmulas (7) y (8), se necesita calcular, aplicando
la regla de la cadena, las derivadas de orden 1, 2 y 3 de la
función f(t, y) = t y:
f '(t, y(t)) = y + t y' = y + t (t y) = y(1 + t2)
f ''(t, y(t)) = y'(1 + t2) + y 2 t = t y (1 + t2) + 2 t y = (3 t + t3) y
f '''(t, y(t)) = (3 + 3 t2) y + (3 t + t3) y' =
(3 + 3 t2) y + (3 t + t3) t y = (3+ 6 t2
+ t4) y
Reemplazando en (5), la fórmula iterativa para el método de Euler
resulta:
|
|
(9) |
Según la fórmula (6), reemplazando las derivadas correspondientes se obtiene la fórmula del método de Taylor de orden 2:
|
|
(10) |
Por último, reemplazando las derivadas en la fórmula (7), resulta la
fórmula del método de Taylor de orden 4:
|
|
(11) |
Con el valor de h = 0,25 se obtuvieron los valores que se muestran en la
tabla, para los métodos de Euler y de Taylor de orden 2 y 4, según las fórmulas
(10) y (11), y los errores absolutos de todos los métodos, respecto
de la solución exacta, que en este caso se puede calcular en forma
analítica, mediante separación de variables.
| t | exacta | Euler | Error Euler | Taylor 2 | Error Taylor 2 | Taylor 4 | Error Taylor 4 |
| 0,00 | 1,00000000 | 1,00000000 | 0,00000000 | 1,00000000 | 0,00000000 | 1,00000000 | 0,00000000 |
| 0,25 | 1,03174341 | 1,00000000 | 0,031743407 | 1,031250000 | 0,000493407 | 1,031738281 | 5,1265E-06 |
| 0,50 | 1,13314845 | 1,0625000 | 0,070648453 | 1,129943848 | 0,003204605 | 1,133103361 | 4,50921E-05 |
| 0,75 | 1,32478476 | 1,1953125 | 0,129472259 | 1,315325260 | 0,009459499 | 1,324639601 | 0,000145158 |
| 1,00 | 1,64872127 | 1,41943359 | 0,229287677 | 1,626173613 | 0,022547658 | 1,648348707 | 0,000372564 |
| 1,25 | 2,18420081 | 1,77429199 | 0,409908819 | 2,134352867 | 0,049847944 | 2,183310836 | 0,000889975 |
| 1,50 | 3,08021685 | 2,32875824 | 0,751458609 | 2,972253113 | 0,107963736 | 3,078122306 | 0,002094543 |
| 1,75 | 4,62395315 | 3,20204258 | 1,421910573 | 4,388717487 | 0,235235665 | 4,618968259 | 0,004984894 |
| 2,00 | 7,3890561 | 4,60293621 | 2,786119891 | 6,865942788 | 0,523113311 | 7,376895196 | 0,012160903 |
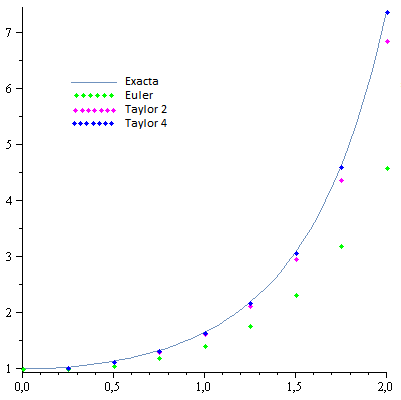
En el siguiente gráfico se pueden ver las soluciones obtenidas con los distintos métodos, y la proximidad a la solución exacta de cada una de ellas.