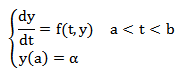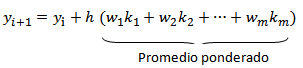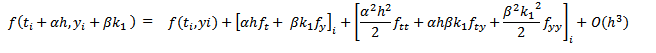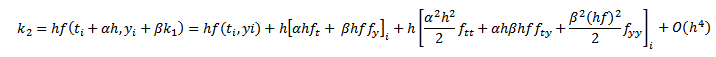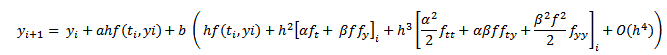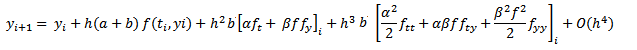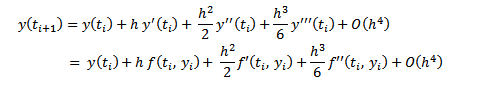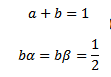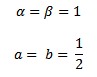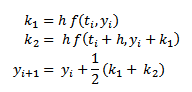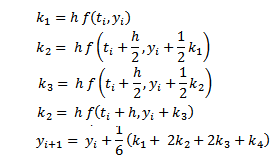Métodos de Runge Kutta

Los métodos de Taylor tienen la propiedad de un error local de truncamiento de orden superior, pero la desventaja de requerir el cálculo y la evaluación de las derivadas de f(t, y). Esto resulta algo lento y complicado, en la mayoría de los problemas, razón por la cual, en la práctica casi no se utilizan. El método de Euler, lamentablemente requiere de un paso muy pequeño para una precisión razonable.

Los métodos de Runge kutta tienen el error local de truncamiento del mismo orden que los métodos de Taylor, pero prescinden del cálculo y evaluación de las derivadas de la función f(t, y).

Se presenta de nuevo el problema de valor inicial cuya solución se intenta aproximar:
 

Como en los métodos anteriores, se determina primero la malla {t₀, t₁, ... , t_N} de paso h, donde t₀ = a y  t_N = b. En estos puntos es donde se va a obtener la aproximación de la solución.

En esencia, los métodos de Runge-Kutta son generalizaciones de la fórmula básica de Euler y_i+1 = y_i + h f(t_i, y_i) en los que el valor de la función f se reemplaza por un promedio ponderado de valores de f en el intervalo t_i ≤ t ≤ t_i+1, es decir,

En esta expresión las ponderaciones w_i, i = 1, ..., m son constantes para las que en general se pide que su suma sea igual a 1, es decir, w₁ + w₂ + ... + w_m = 1, y cada k_j es la función f evaluada en un punto seleccionado (t, y) para el cual t_i ≤ t ≤ t_i+1. Se mostrará que los k_j se definen en forma recursiva.

Se define como orden del método al número m, es decir, a la cantidad de términos que se usan en el promedio ponderado.

Runge-Kutta de primer orden

Si m = 1, entonces se toma w₁ = 1 y la fórmula (2) resulta

Igualando esta fórmula al desarrollo de Taylor de orden 1 de la función y(t), alrededor del punto t_i, y calculado en el punto t_i+1: 

y teniendo en cuenta que y_i @ y(t_i), resulta k₁= f(t_i, y_i), obteniendo así la fórmula de Euler y_i+1 = y_i + h f(t_i, y_i). Por lo tanto, se dice también que el método de Euler es un método de Runge Kutta de primer orden.

Runge-Kutta de segundo orden

Ahora se plantea, con m = 2, una fórmula del tipo:

donde

y las constantes a, b, a, b se deben determinar, de manera que la expresión (5) coincida con el desarrollo de Taylor de y de orden más alto posible.

Para ello, utilizando un desarrollo de Taylor para funciones de dos variables, tenemos que:

donde el subíndice i indica que todas las derivadas están evaluadas en el punto (t_i, y_i).

Reemplazando k₁ y teniendo en cuenta la expresión de k₂, usando (7) tenemos que:

agrupando los términos de (8) por las potencias de h, y reemplazando en la expresión (5) el valor de k₁ y  k₂, resulta

Por otro lado, se hace un desarrollo de Taylor de orden 3 de la función y(t), calculado en el punto t_i+1, obteniendo:

Aplicando regla de la cadena para las derivadas de f, se tiene:

Comparando las expresiones (10) y (12), e igualando los coeficientes de h y h², se tiene:

Sucede que se tienen cuatro incógnitas, pero tres ecuaciones, con lo que queda un grado de libertad en la solución del sistema dado en (13). Se trata de usar este grado de libertad para hacer que los coeficientes de h³ en las expresiones (10) y (12) coincidan. Esto obviamente no se logra para cualquier f.

Hay muchas soluciones para el sistema (13), una de ellas es

obteniendo así la siguiente fórmula, del método de Runge Kutta de orden 2:

para i desde 0 hasta N-1, tomando un mallado {t_i, i = 0, .., N}

Este método tiene un error local de O(h³), y global de O(h²).

Mejora entonces el método de Euler, por lo que se espera poder usar con este método un paso mayor. El precio que debe pagarse en este caso, es el de evaluar dos veces la función en cada iteración.

De la misma manera que se realizó arriba, se pueden derivar fórmulas de Runge-Kutta de cualquier orden, pero estas deducciones resultan excesivamente complicadas. Una de las más populares, y más utilizada por su alta precisión, es la de orden 4, que se presenta a continuación.

Runge-Kutta de cuarto orden

Si ahora m = 4, se obtiene, con un desarrollo del tipo del anterior, la siguiente fórmula, para i desde 0 hasta N-1:

Si bien con facilidad se pueden deducir otras fórmulas, el algoritmo expresado en (16) se denomina método de Runge-Kutta de cuarto orden, o método clásico de Runge-Kutta, abreviado como RK4. Este algoritmo es de uso extendido, y reconocido como una valiosa herramienta de cálculo, por la buena aproximación que produce.

Esta fórmula tiene un error de truncamiento local de O(h⁵), y un error global de O(h⁴).  De nuevo, el precio que se debe pagar por la mejora en el error, es una mayor cantidad de evaluaciones de la función, resultando en un mayor tiempo de cálculo si la función es complicada. Tiene la ventaja, sobre el método de Taylor de orden 4 (cuyo error global es también O(h⁴), que no requiere el cálculo de las derivadas de f.

Implementación del método RK4

Se presenta a continuación el pseudocódigo del método RK4, para ser implementado en cualquier lenguaje de programación, o software simbólico.

Ejemplo

Con el método RK4, obtener una aproximación del valor de y(1,5) para el siguiente problema de valor inicial, tomando un paso h = 0,1.

El primer paso para resolver este problema es determinar la malla de puntos en donde se va a obtener la solución.

Como en este caso h está dado, se tiene que N = (1,5 - 1)/0,1 = 5.

Por lo tanto, los puntos en donde se va a determinar la solución, dados por la fórmula ti = 1 + 0,1 i, para i =1,2,3,4,5, son:

t₁ = 1,1
t₂ = 1,2
t₃ = 1,3
t₄ = 1,4
t₅ = 1,5

Una vez establecida la malla del problema, tenemos, para i = 0:

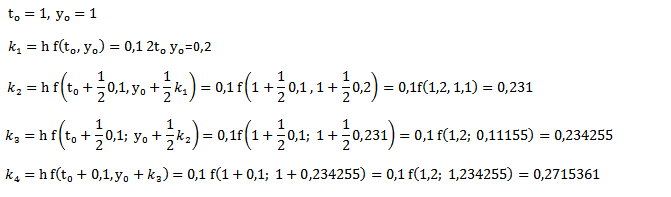
Resulta entonces,

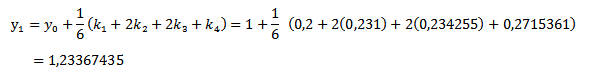
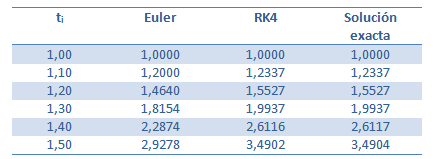
y aplicando sucesivamente la fórmula de RK4, para i desde 1 hasta 4, se obtienen los datos que se muestran en la siguiente tabla, donde además se muestra el valor de la solución exacta para cada punto de la malla.

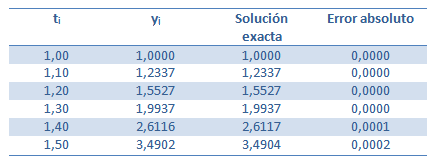
Al analizar la tabla anterior y comparar los resultados obtenidos con el método RK4 con los valores reales, se ve por qué es tan difundido este método. En la próxima tabla se comparan los métodos de Euler y Runge Kutta de orden 4 para el mismo problema.