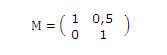Las transformaciones lineales T: R1 ® R1 son multiplicaciones por un escalar. En dimensiones superiores pueden presentarse otras situaciones. Veremos aquí transformaciones lineales T: R2 ® R2 con nombre propio: rotaciones, reflexiones, expansiones y deslizamientos.
Para poder analizar el efecto geométrico de las transformaciones, se ha dibujado una circunferencia de radio unitario, con degradé de colores.

Cuando se rotan los vectores (1, 0) y (0, 1) un ángulo q, se obtienen respectivamente, los vectores (cos q, sen q) y (-sen q, cos q). Así, una transformación de rotación se representa matricialmente con:
![]()
Ejemplos
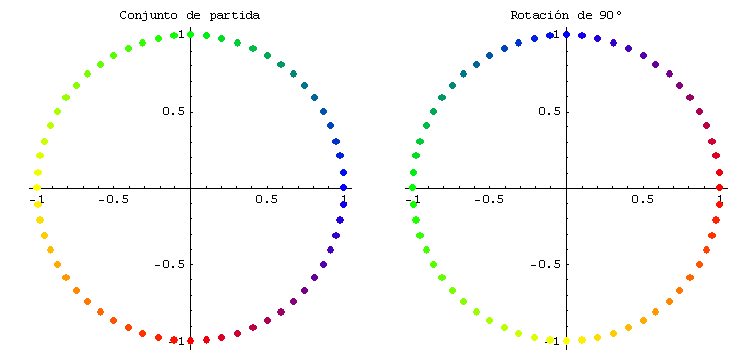
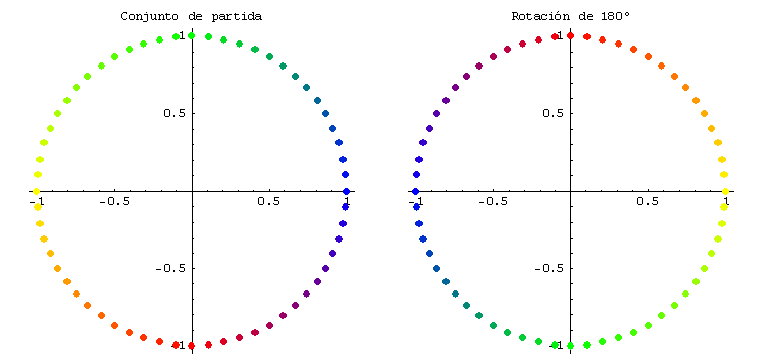
Cuando se aplican transformaciones lineales de TA:R2 ® R2 y TB:R2 ® R2 de matrices:
![]()
se obtienen, respectivamente, rotaciones de 90° y 180°. Gráficamente:

Para cada recta que pasa por el origen de coordenadas, existe una transformación lineal que refleja el plano respecto de esa recta.
Aquí mostraremos tres reflexiones: respecto del eje x, del eje y, y de la recta y = x
Ejemplos
Cuando se aplican transformaciones lineales de TA:R2 ® R2, TB:R2 ® R2 y TC:R2 ® R2 de matrices:
![]()
se obtienen, respectivamente, la reflexión respecto del eje x, la reflexión respecto del eje y, y la reflexión respecto de la recta y = x. Gráficamente:
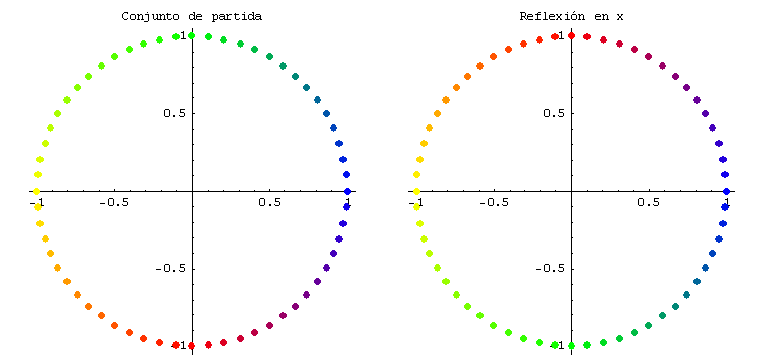
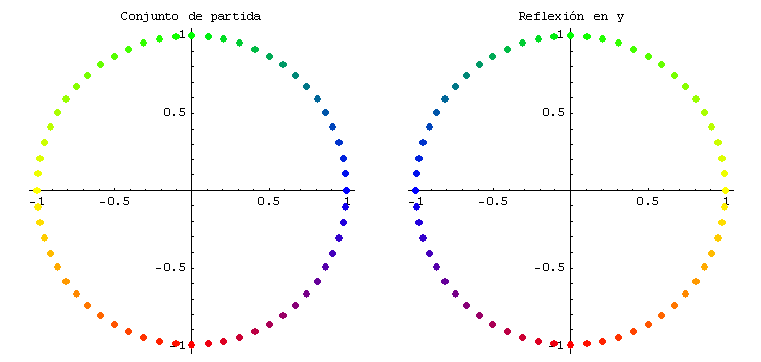
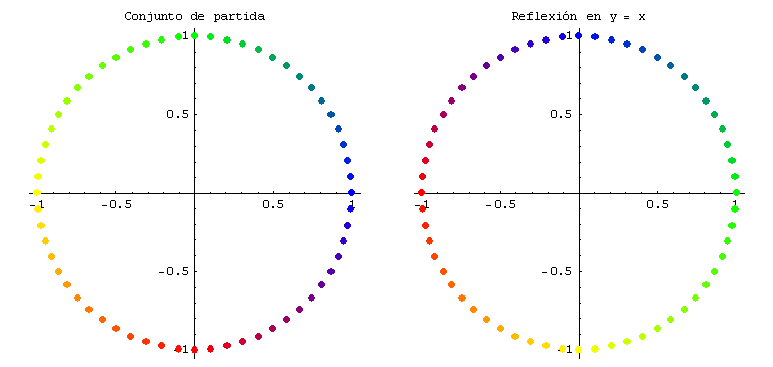

La expansión a lo largo del eje x es una transformación lineal que a cada (x, y) del dominio le hace corresponder (c x, y). La constante c se denomina factor de expansión y es c > 1.
La compresión a lo largo del eje x es una transformación lineal que a cada (x, y) del dominio le hace corresponder (c x, y). La constante c se denomina ahora factor de compresión y es 0 < c < 1.
Las expansiones o compresiones a lo largo del eje y son transformaciones lineales que a cada (x, y) del dominio le hace corresponder (x, c y).La constante es c > 1 para las expansiones y 0 < c < 1 para las compresiones.
Ejemplos
Se muestran gráficamente una expansión en x (con c = 2) y una compresión en y (con c = 0,5)
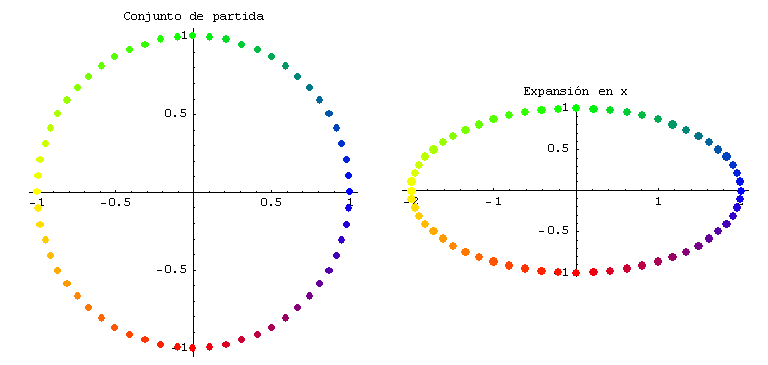
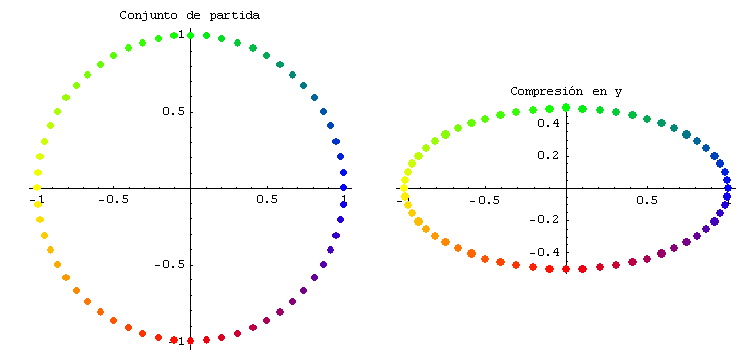

Un deslizamiento a lo largo del eje x es una transformación lineal que a cada (x, y) del dominio le hace corresponder (x + c y, y), donde c es una constante que puede ser positiva o negativa.
Un deslizamiento a lo largo del eje y es una transformación lineal que a cada (x, y) del dominio le hace corresponder (x, c x + y), donde c es una constante que puede ser positiva o negativa.
Ejemplos
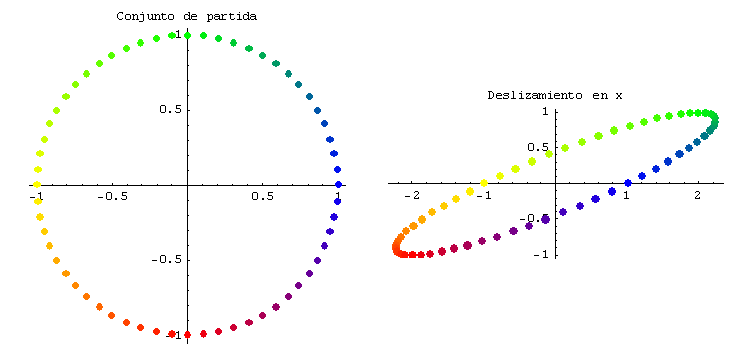
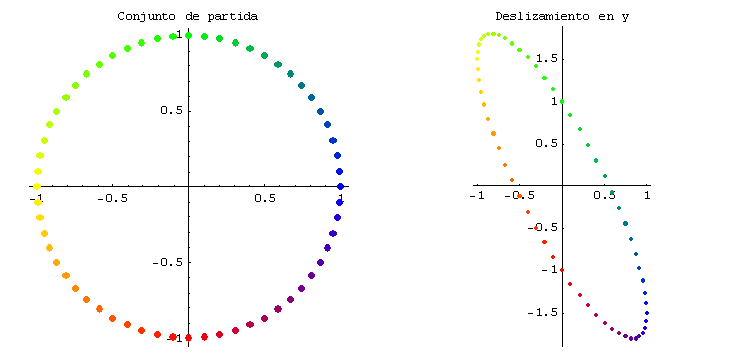
Se muestran gráficamente un deslizamiento a lo largo del eje x (con c = 2) y un deslizamiento a lo largo del eje y (con c = - 1,5)
Los caricaturistas y
las transformaciones lineales
Extraído de Algebra
Lineal con aplicaciones, de George Nakos y David Joyner

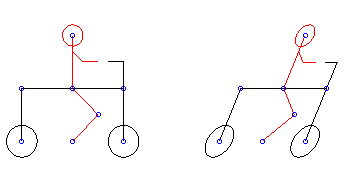
Muchas veces los caricaturistas utilizan transformaciones lineales para lograr movimientos en sus dibujos. Por ejemplo, supóngase que se desea hacer un deslizamiento en la dirección del eje x, del ciclista que se muestra a la izquierda en la siguiente figura. Basta con multiplicar los puntos por la matriz M, para obtener la imagen de la derecha.