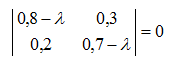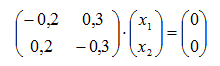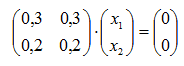Así como los sistemas de ecuaciones lineales se utilizan en la resolución de sistemas estáticos, es decir, en sistemas que no dependen del tiempo, los autovalores y autovectores se utilizan principalmente en la solución de sistemas dinámicos, esto es, en sistemas que son función del tiempo. Para ejemplificar, se analizará el siguiente ejemplo.

Una empresa de publicidad encargada de la propaganda de un supermercado A, determina que del total de clientes que compran en el supermercado A un fin de semana, el 80% vuelve a comprar en A el siguiente fin de semana, mientras que el 20% restante va a comprar al supermercado B. Se sabe también que del total de clientes que compra en B un fin de semana, el 70% vuelve a comprar el fin de semana siguiente en ese supermercado y el 30% restante va al supermercado A. ¿Cuál es la distribución de clientes luego de ocho fines de semanas siguientes al estado inicial?

Esta situación puede plantearse en forma matricial como:

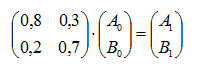
donde:

	es el estado inicial del sistema
	es el porcentaje de clientes que compra en el supermercado A y B respectivamente, al fin de la semana inicial
	es el estado del sistema al fin de semana siguiente, S1
	es el porcentaje de clientes que compra en el supermercado A y B respectivamente, el fin de semana siguiente.
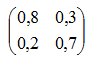	es la matriz de transición que nos permite pasar del estado S0 al estado S1

Luego, el estado del sistema S₂ se obtiene repitiendo el procedimiento anterior:

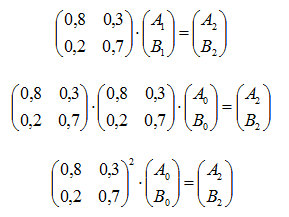
Por último, el estado del sistema n fines de semana luego del estado inicial considerado es:

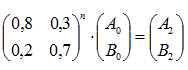
Por lo tanto, para encontrar el estado S₈ del sistema se debe calcular la potencia octava de la matriz de transición. Realizando algunas operaciones, se obtiene:

Si el estado inicial del sistema es:

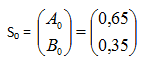
es decir, el supermercado A tiene 65% de los clientes y el supermercado B tiene el 35% de los clientes, luego de ocho fines de semanas siguientes al estado inicial, la distribución de clientes se estabiliza en los siguientes porcentajes:

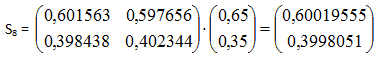
De esta manera, se puede concluir que el supermercado A tiene aproximadamente el 60% de los clientes y el supermercado B, el 40%.
De los resultados obtenidos surge el siguiente interrogante: ¿existe alguna forma eficiente de calcular la potencia enésima de la matriz de transición sin necesitad de realizar tantos cálculos tediosos?
Para describir la evolución de un sistema dinámico, como ya se ha visto, se deben calcular potencias de matrices cuadradas. Si se considera el sistema cuyo estado en el tiempo k está representado por el vector columna x y sea A Є R^nxn la matriz de cambio de estado, el estado del sistema en el tiempo k+1 será:
 

A . x_k = x_k+1

En el tiempo k+2, el estado del sistema será:

A . x_k+1 = x_k+2

A . x_k+1 = A. (A . x_k ) = A² . x_k = x_k+2

Y si se repite el procedimiento, se obtiene:

A^p . x_k = x_k+p

Es decir, el estado del sistema en el tiempo k+p será A^p veces el estado del sistema en el tiempo k.
Además, es conveniente poder predecir cómo evolucionará el sistema en períodos grandes, es decir, cuando p → ∞.

Para resolver estas cuestiones, resulta conveniente encontrar una forma eficiente de calcular potencias de matrices para poder determinar A^p cuando p→∞.

¿Será posible encontrar una matriz diagonal D que sea semejante a la matriz A para calcular las potencias de la matriz A a parir de las potencias de la matriz D?

Para calcular la potencia enésima de una matriz A Є R^nxn, se diagonalizará la matriz A. Teniendo en cuenta que P^-1 A P = D, resulta:

P P^-1 A P P^-1 = P D P^-1

A = P D P^-1

Y para calcular potencias de A,

A² = (P D P^-1) (P D P^-1) = P D (P^-1 P) D P^-1 = P D I D P^-1 = P D² P^-1

Repitiendo el procedimiento, se obtiene:

Aⁿ = P Dⁿ P^-1

El cálculo de potencias de una matriz diagonal es sencillo:

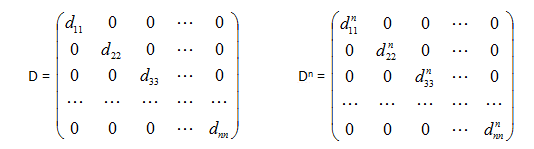
es decir, basta con elevar a la n cada elemento de la diagonal principal.

Volviendo nuevamente al problema inicial, es decir, calcular la distribución de clientes luego de ocho fines de semanas siguientes al estado inicial, es ahora fácil determinar su solución. Para ello, diagonalizaremos la matriz A.

Para obtener la matriz diagonal D, se calcularán los autovalores asociados a la matriz A.

Para calcular los autovectores para cada autovalor, es necesario resolver el siguiente sistema de ecuaciones:

Si λ₁ = 1 , resulta:

La solución de (2) son vectores de la forma  (x₁, 2/3 x₁)^t . Por lo tanto, un autovector correspondiente a λ₁ = 1 es (1, 2/3)^t.

Si λ₂ = 0,5 , resulta:

La solución de (3) son vectores de la forma  (x₁, -x₁)^t . Luego, un autovector correspondiente a λ₂ = 0,5 es (1, -1)^t.

Entonces, la matriz P que diagonaliza a la matriz A y su inversa son:

La matriz D diagonal similar a la matriz A es, entonces:

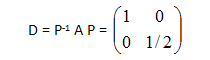
Luego, resulta:

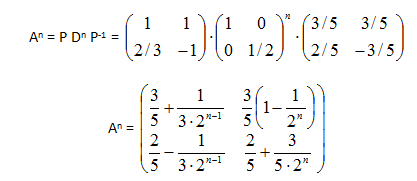
Recordando que el estado inicial del sistema es S₀ = (0,65, 0,35)^t , la distribución, en porcentajes, de clientes luego de n semanas será:

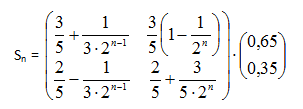
De esta manera, los porcentajes de clientes de cada supermercado cuando n es muy grande, n→∞, será:

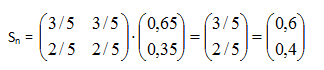
Así, se tiene que al supermercado A concurrirá el 60% de los clientes y al supermercado B concurrirá el 40% de los clientes.