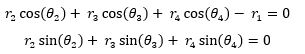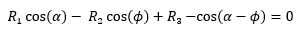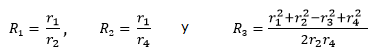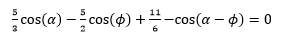Un mecanismo de cuatro barras articuladas puede modelarse mediante una función no lineal. Considerando una de las barras sobre el eje x, el mecanismo es el que se muestra en la figura.

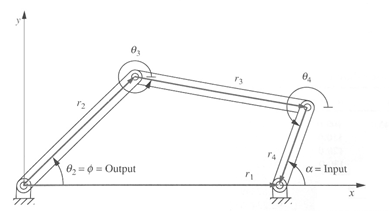
 El ángulo  a es la entrada del mecanismo, y el ángulo f la salida. A partir de la ecuación vectorial

donde r₁ es el vector que yace sobre el eje x, se puede obtener una relación entre los ángulos a y f. Para lograrlo, se debe escribir la ecuación (1) como dos ecuaciones escalares, correspondientes a las componentes x e y de los vectores r. Entonces,

Combinando las ecuaciones (2.a) y (2.b), haciendo q₂ = f  y q₄ = a + p, y simplificando, se llega a la ecuación de Freudensteien:

donde

Considerando el mecanismo de cuatro barras articuladas especificado por r₁ = 10, r₂ = 6, r₃ = 8 y r₄ = 4, la ecuación (4) resulta:

Como puede verse en la ecuación (5), los ángulos  a y f están relacionados de forma no lineal. Por lo tanto, para obtener f para un valor dado de a, debe resolverse una ecuación no lineal.

A continuación, se brinda una herramienta para obtener una aproximación de este ángulo. Los datos del problema se seleccionan de las listas desplegables a la izquierda de la ventana. Los valores de las barras precargados satisfacen la regla de Grashof: la suma de las longitudes de la barra más corta y de la más larga ( 4 y 1) no puede ser mayor que la suma de las otras dos (2 y 3).

Bibliografía: Numerical Methods for Engineers and Scientists. J. Hoffman. Mc Graw – Hill (1992)