Se puede observar que:

•  La gráfica de h(x) = -f(x) se obtiene por simetría axial de eje x.
   
• Para el caso de

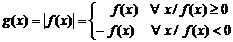
la gráfica se obtiene de la siguiente forma:

• "x / f(x) ≥ 0 las gráficas de f y de g coinciden

• "x / f(x) ≤ 0 la gráfica de g coincide con la de -f(x)
   

• Para obtener la gráfica de j(x) = f(-x) a partir de la de f(x), se realiza una simetría de eje y

Muevan el deslizador para observar la gráfica de la función opuesta y analicen: La función h, ¿conserva los ceros de f ? Si la función f fuera par, ¿la h también lo sería? ¿Si fuese impar? ¿Se conserva el crecimiento? Si la función f fuera inyectiva, ¿la h también lo sería? ¿Cómo es el dominio de h(x) con respecto al de f(x)? Muevan el deslizador para observar la gráfica de la función valor absoluto y analicen: La función g, ¿conserva los ceros de f ? Si la función f fuera par, ¿la g también lo sería? ¿Si fuese impar? ¿Se conserva el crecimiento? Si la función f fuera inyectiva, ¿la g también lo sería? ¿Cómo es el dominio de g(x) con respecto al de f(x)? Muevan el deslizador para observar la gráfica de la función de variable opuesta y analicen: La función j, ¿conserva los ceros de f ? Si la función f fuera par, ¿la j también lo sería? ¿Si fuese impar? ¿Se conserva el crecimiento? Si la función f fuera inyectiva, ¿la j también lo sería? Si el dominio de f(x) fuera el conjunto R+, ¿Cuál sería el dominio de j(x)?